Mathematical functions have applications in everyday life. The operation of a soda vending machine is a good example used to explain mathematical functions. Depending on how much money you deposit, you can choose from a variety of beverages. Similarly, while using functions, you can enter different integers and get back new ones.
The inputs you can use are represented by the domain. Your options for outputs are represented by the range. Get familiar with locating a function's domain and range and graphing them using this article.
Domain and range
The sets of all the x- and y-coordinates of ordered pairs, respectively, define a relation's domain and range. For instance, if the relationship is R = {(1, 2), (2, 2), (3, 3), and (4, 3)}, then
The collection of all x-coordinates with values {1, 2, 3, 4} is known as the domain.
The range is y-coordinates and in this example, the set is {2, 3}.
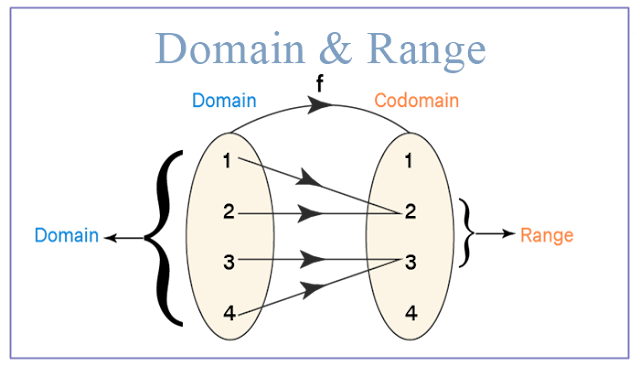
Domain and range of a function
Functions are made up of various parts, including their domain and range. All input values that are possible is domain. Output values that are possible are included in range. Domain->Function->Range is the order of representation. If a function f: A->B exists in which each element in set A is mapped to an element in set B, then set A is the domain, and set B is the co-domain. When (a,b) is contained in R, the image of element 'a' under the relation R is supplied by 'b.' The collection of images makes up the function's range. A function's domain and range are generally denoted using symbols.
Domain(f) = {x contained in R: Condition} to denote range, you use Range(f) = {f(x): x domain(f)}
Finding the domain of a function
Applying one of the domain-finding rules according to the type of function is all that is necessary to determine a function's domain. Here are some examples:
Example 1: you use a rule to determine the domain of a function f(x) = √ (x + 3). Next, you obtain x + 2≥ 0. You obtain x≥ -2 after solving this inequality. Consequently, the range of f(x) is [-2, ∞).
Example 2: Another rule is used to determine the domain of the function g(x) = (2x + 1) / (x - 2). Thus, you obtain x - 2 ≠ 0. Solving this gives you x ≠ 2. Its domain is, therefore, the set of all real numbers other than 2, which can be expressed as (-∞, 2) ∪ (2, ∞) in interval notation.
Finding the range of function
The rules can be applied to determine the range of a function if it exists in one of the functions listed in the given problem. In either case, you can graph it and determine the range by examining the range of y values that the graph covers. Here are some examples:
A common rule is used in Example 1 to determine the range of the function f(x) = 2 (x - 3)2 - 5. The range is then y≥ -5 (or) [-5, ∞).
Example 2: Using another rule to determine a function's range, g(x) = ln (2x - 3) + 4 yields results. The set of all real numbers (R) is its range.
Final thoughts
In simple terms, the domain of a function is the set of all potential inputs, whereas the range of a function is the set of all possible outputs. Understanding domain and range is simple, but it does require some practice to become proficient.
No comments:
Post a Comment